Matemalescopio

matemáticos... no tienen sus misterios y, lo que es más, sus repugnancias y contradicciones?

G.Berkeley

 Matemáticos que han nacido o fallecido el día 12 de Marzo

Curiosidades del día

• Hoy es el septuagésimo segundo día del año.
• 72 es un número pronic u oblongo, producto de dos enteros consecutivos.
• 72 es el menor número cuya potencia quinta es suma de cinco potencias quintas 72⁵=19⁵+43⁵+46⁵+47⁵+67⁵.
• La regla del 72 se utilizó en banca como una aproximación para saber el tiempo que tarda una inversión en duplicarse al r%.Para una inversión al 5% tardaría 72/5=14,4 años. La regla se basa en una aproximación del ln2.
• El rombicuboctaedro es un sólido de Arquímedes con 72 aristas, tiene 12 caras que son cuadrados, 8 caras que son hexágonos, y seis caras que son octógonos, para un total de 26 caras en total.
• 72 la suma de cuatro números primos consecutivos (13 + 17 + 19 + 23), así como la suma de seis números primos consecutivos (5 + 7 + 11 + 13 + 17 + 19)
• 72 es el número más pequeño que se puede expresar como la diferencia de los cuadrados de primos consecutivos de dos formas distintas: {19² - 17² } y {11² - 7² }
• 72 es 2³ + 3². Es el número más pequeño donde los números son primos distintos.
• En un plano, el pentágono regular tiene ángulos exteriores de 72^o
• 72 es un número abundante pues es menor que la suma de sus divisores propios.
• 72 es un número odioso pues en su expresión binaria aparece un número impar de unos.
• 72 es un número poderoso pues cualquier primo divisor de 72, su cuadrado también lo es.
• 72 es un número práctico pues todos los números menores que él son suma de divisores de 72.
• 72 es un número de Ulam, es un miembro de una secuencia entera, la cual fue concebida por el matemático polaco Stanislaw Ulam y publicada en SIAM Review en 1964. La secuencia estándar de Ulam comienza con U1=1 y U2=2, siendo los primeros dos números de Ulam. Entonces, para n > 2, Un queda definido como el entero más pequeño que es la suma de dos miembros anteriores diferentes entre sí en exactamente una forma.

Tal día como hoy del año:

• 1610, Galileo dedica su Sidereus nuncius al Gran duque Cosmos II.
• 1615, Castelli informó a Galileo que el arzobispo de Pisa le había exigido que renunciara a la carta que le había enviado, que era la base de un cargo de herejía
• 1832, Faraday escribió una carta secreta prediciendo la existencia de ondas electromagnéticas. Faraday presentó su carta al secretario de la Royal Society de Londres, donde permaneció durante más de un siglo en una caja fuerte
• 1926, John von Neumann, de 22 años, recibió su doctorado summa cum laude en matemáticas con especialización en física y química experimental de la Universidad de Budapest
• 2009, La Cámara de Representantes de Estados Unidos aprobó una resolución no vinculante (HRES 224), reconociendo el 14 de marzo de 2009 como el Día Nacional de Pi

Cimmino 

El matemático italiano Gianfranco Louis Joseph Cimmino  es conocido por sus contribuciones al estudio de las ecuaciones diferenciales parciales de tipo elíptico y al análisis numérico

Trabajó en el  Instituto de Matemática Aplicada (INAC) y fue uno de los cuatro asistentes de  Picone, junto con Renato Caccioppoli , Carlo Miranda y José Scorza Dragoni .

 Patodi

El matemático indio Vijay Kumar Patodi hizo contribuciones fundamentales a la geometría diferencial y la topología . Él fue el primer matemático en aplicar los métodos de la ecuación del calor  para la prueba del teorema del índice de operadores elípticos.  Fue profesor en el Instituto Tata de Investigación Fundamental , Mumbai (Bombay) .

Patodi se doctoró en  la Universidad de Bombay , bajo la dirección de MS Narasimhan y Ramanan en el Instituto Tata de Investigación Fundamental . 

Las bases de su doctorado son dos documentos, "Curvature and Eigenforms of the Laplace Operator", y "uAnalytical Proof of the Riemann-Roch-Hirzebruch Formula for Kaehler Manifolds". 

Pasó entre los años del  1971 al 1973 en el Instituto de Estudios Avanzados en Princeton , Nueva Jersey , donde colaboró ​​con Michael Atiyah , Isadore Singer, y Raoul Bott . El trabajo conjunto llevó a una serie de artículos, "Spectral Asymmetry and Riemannian Geometry"  con Atiyah y Singer, en los se definió  el η -invariante . Este invariante iba a jugar un papel importante en los avances posteriores en la década de 1980.

Patodi fue ascendido a profesor titular en el Instituto Tata de 30 años de edad, sin embargo, murió a los 31 años, como consecuencia de las complicaciones antes de la cirugía de trasplante de riñón. 

El matemático alemán Karl Wilhelm Feuerbach  trabajó esencialmente en geometría euclídea y proyectiva, en paralelo a los trabajos de Poncelet, haciendo una clara distinción entre  propiedades afines y proyectivas. Publicó Propiedades de algunos puntos distinguidos del triángulo rectilíneo(1822), en donde expuso las características del círculo de los nueve puntos (estos puntos son los pies de  las  perpendiculares  trazadas  desde  los  vértices  sobre  los  lados  opuestos,  los  puntos  medios  de  los  lados  y  los  puntos  medios  de  los  segmentos  que  unen  los  vértices  con  el  ortocentro).  Feuerbach  demostró que el centro de dicho círculo está situado sobre la recta de Euler del triángulo, coincidiendo con el punto medio del segmento que une el ortocentro y el circuncentro, Además demostró que dicha circunferencia   es   tangente   interior   a   la   circunferencia   inscrita,   y   tangente   exterior   a   las   tres   circunferencias  exinscritas  (Coolidge  dijo  que  esta  demostración  es  la  más  bella  de  la  geometría  elemental  descubierta  desde  la  época  de  Euclides)

Feuerbach fue especialista en geometría del triángulo, muy en boga en la época e,  independientemente de Möebius y Plücker, fue uno de los promotores de las coordenadas homogéneas en el plano proyectivo, comparables a las baricéntricas en el plano afín

El matemático y físico suizo Johan Jakob Balmer es conocido por haber decodificado la sucesión lógica 656, 486, 434, 410, ... Se trata de las longitudes de ondas de los cuatro rayos en el espectro visible del hidrógeno.

Balmer estableció empíricamente que estas cuatro longitudes de onda (que constituyen la serie de Balmer), podían expresarse mediante una fórmula, la fórmula de Balmer 

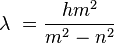
La justificación de esta fórmula sólo se ha obtenido posteriormente con la física cuántica. ¿ cuál es el término siguiente a 410? 

El matemático italiano Ernesto Cesaro es conocido por sus contribuciones a la geometría diferencial y a la teoría de series infinitas.

Entre sus otros trabajos se  incluyen Introducción a la teoría matemática de los cálculos infinitesimales ( 1893 ), Análisis Algebraica ( 1894 ), Elementos de cálculo infinitesimal ( 1897 ). Propuesta de una definición de una suma de un serie , conocida hoy como Suma de Cesàro , propuesta por el límite de la media aritmética de la suma de los términos parciales de la sucesión. La suma de Cesàro coincide con la suma habitual en el caso de series convergentes, pero también existe para una clase de serie no convergente.

En teoría de números nos ha dejado el llamado teorema de Cesaro:

Sean p y q dos números enteros elegidos aleatoriamente. La probabilidad para que p y q sean primos entre si es 6/pi²

Murió al intentar salvar a su hijo menor de ahogarse 

El matemático, astrónomo, economista  y estadístico americano Simon Newcomb descubrió, en 1881,  el principio estadístico conocido como ley de Benford o ley del primer número. En el se apercibe que las primeras páginas de las tablas de logaritmos son más usadas que las siguientes. Eso le lleva a formular el principio que para toda lista de números tomados en un conjunto de datos arbitrarios, la primera cifra es uno con muchas más frecuencia

Berkeley

El filósofo irlandés George Berkeley era profundamente religioso, dedicó su obra a fundar la fe en el discurso racional, a contracorriente del espíritu librepensador de su época, que, con el auge del empirismo, había quedado marcada por un cierto escepticismo. Tras estudiar en Dublín y ordenarse sacerdote, en 1710 escribió su obra fundamental titulada Los principios del conocimiento humano, y en 1734 fue nombrado obispo anglicano de Cloyne (al sur de Irlanda).

Berkeley adoptó desde el principio un inmaterialismo que lo enfrentó a Hobbes y a Locke: según él, afirmar que las cosas existen independientemente de nuestra percepción implica una contradicción, sobre todo desde un empirismo consecuente. En efecto, si no debemos aceptar nada sobre lo que no exista una certeza absoluta, y puesto que de las cosas «sólo conocemos su relación con nuestros sentidos», no lo que son en sí mismas, únicamente podemos aceptar como ciertas las representaciones mentales. 

Berkeley inauguró con ello el principio del idealismo, según el cual «el ser» de las cosas es su «ser percibidas», de tal modo que la sustancia no es ya la materia, sino únicamente la sustancia espiritual, de cuya existencia nuestros pensamientos son la prueba irrefutable, de acuerdo con su contemporáneo Descartes. Sin embargo, si los objetos no existen como fundamento de nuestras representaciones mentales, tenía que haber algo existente que, permaneciendo fuera de nuestra mente, suscitase nuestras percepciones, un principio que Berkeley halló en Dios. 

Como producto de su radicalización del empirismo, Berkeley tuvo que redefinir el concepto de causa. Así, consideró que las causas físicas no eran verdaderas causas, sino únicamente signos que la ciencia debía interpretar para asegurar la supervivencia. La filosofía de Berkeley tuvo escasa aceptación entre sus contemporáneos, a pesar de sus esfuerzos por hacerla más popular y accesible en Los tres diálogos entre Hylas y Philonus (1713).

En 1734 publicó El analista, una crítica a los fundamentos de la ciencia, que fue muy influyente en el desarrollo de la matemática.

El analista o Un discurso dirigido a un matemático infiel (el «infiel» era Edmund Halley), calificada por Florian Cajori, historiador de las matemáticas, como «el hecho más espectacular del siglo en la historia de las matemáticas británicas».

Después de su critica, salieron en defensa de Newton, entre otros, James Jurin, de Cambridge; John Walton, de Dublin, y Colin Maclaurin, de Escocia. Berkeley respondió a Jurin con una punzante sátira en Una defensa del libre pensamiento en matemáticas (1735); en un apéndice del mismo trabajo le contestó a Walton y lo hace de nuevo en Razones para no contestar...

 Mordell

El matemático inglés Louis Joel Mordell realizó sus estudios superiores con Hardy. estudió particularmente las ecuaciones diofánticas  y más generalmente las ecuaciones algebraicas que admiten soluciones racionales, lo que supone el estudio de curvas algebraicas con coordenadas racionales.

Estudió en particular la ecuación y²=x³+k donde k es un parámetro entero dado y (x,y) y en Z²

La curva asociada es una curva elíptica cuyo estudio está ligado, como la conjetura de Mordell,  a la célebre conjetura de Fermat, conocida hoy como teorema de Fermat-Wiles.

La conjetura de Mordell:

Una curva algebraica de género al menos 2, no puede admitir mas que un número finito de puntos de coordenadas racionales

fue probada en 1983 por un joven matemático alemán,  Gerd Faltings 

Cesari

El matemático italiano Lamberto Cesari se graduó en la  Universidad de Pisa bajo la dirección de LeonidaTonelli . Más tarde estudió en Alemania . Luego regresó a Pisa durante un año y luego se trasladó a Roma al  Instituto Nacional de Matemática Aplicada , dirigida por Mauro Picone .

Desde 1938 fue profesor en la Universidad de Pisa. En 1947 fue profesor de análisis de la Universidad de Bolonia . En 1948 se trasladó a los Estados Unidos .

Después de enseñar durante un tiempo en el  Instituto de Estudios Avanzados en Princeton , enseñó en la Universidad de Purdue en Lafayette , de la Universidad de California en Berkeley y la Universidad de Wisconsin en Madison . En 1960 fue profesor en la Universidad de Michigan en Ann Arbor. En 1976 se convirtió en ciudadano estadounidense , pero siguió manteniendo estrechos contactos científicos con la comunidad matemática italiana.

Se le recuerda por sus investigaciones sobre el problema de la constante de Lebesgue de las superficies paramétricas y los problemas variacionales conectados a él.

Escribió cerca de 250 publicaciones científicas que se ocupan de análisis funcional no lineal, así como tres libros de importancia fundamental:

• Superficie ( 1956 )
• Comportamiento asintótico y problemas de estabilidad en las ecuaciones diferenciales ordinarias (1.959 )
• Optimización de la Teoría y Aplicaciones. Problemas con ecuaciones diferenciales ordinarias(1983) 

Lyudmila Vsevolodovna Keldysh

La matemática rusa Lyudmila Vsevolodovna Keldysh comenzó a trabajar en matemáticas en el equipo de Nikolai Nikolaevich Luzin y publicó sus primeros trabajos –de una larguísima lista– en 1934. En 1941 defendió su tesis doctoral bajo la dirección de Luzin. Trabajó en teoría de conjuntos y topología, comenzando con la teoría descriptiva de conjuntos, en especial la estructura de los conjuntos de Borel. Después se dedicó a la topología geométrica, en la escuela de Moscú de Pavel Alexandrov. Se casó en segundas nupcias con el también matemático Petr Sergeevich Novikov (1901-1975): uno de los cinco hijos que tuvo este matrimonio–Sergei Petrovich Novikov– recibió la medalla Fields en 1970.

El matemático italiano Leonida Tonelli se dedicó, como sus maestros Pincherle y Arzela, al análisis a través del cálculo de variaciones y a la teoría moderna del cálculo integral ( en la linea de la medida de Lebesque) a instancias de sus amigos Fubini y Volterra. Profesor de las universidades de Bolonia y Pisa. Tras escribir un gran número de artículos desde 1911 dedicados al cálculo de variaciones, publicó su obra Fundamentos del cálculo de variaciones (2 volúmenes, 1922, 1924), donde enfoca el tema desde el  punto  de  vista  de  los  funcionales.  La  teoría  clásica del  cálculo  de  variaciones  se  basaba  principalmente  en  la  teoría  de  ecuaciones  diferenciales,  mientras  que Tonelli  reemplaza  los  teoremas  de existencia para ecuaciones diferenciales por los de existencia para minimizar integrales de curvas. En  su  obra,  el  concepto  de  semicontinuidad  inferior  de  un  funcional  es  el concepto fundamental,  porque los funcionales no pueden ser continuos. Tonelli considera en primer lugar conjuntos de curvas y  da  teoremas  que  aseguran  la  existencia  de  una  curva  límite  de  una  cierta  clase  de  curvas

Kirchhoff

El físico  y  matemático  alemán ,  Gustav  Robert  Kirchhoff nació  en  Königsberg  (hoy, Kaliningrado, Rusia).  Fue  “privatdozent”  en  la  Universidad  de  Berlín  (1847)  y  tres  años  después  fue profesor  extraordinario  de  física  en  la  Universidad  de  Breslau.  En  1854  fue  profesor  de física  en  la  Universidad  de  Heidelberg,  donde  trabajó  con  Bunsen,  descubriendo  el  cesio (1860)  y  el  rubidio  (1861).  Analizó  el  espectro  de  la  luz  solar.  Fue  profesor  de  física matemática  en  la  Universidad  de  Berlín (1875). Formuló (1845) las leyes que llevan su nombre, sobre la distribución de las corrientes eléctricas.  En  relación  con  las  ecuaciones  de  D ́Alembert-Euler  referentes  a  una  función  analítica         w  =  u+  vi,  es  decir,  ∂u/∂x  =  ∂v/∂y, ∂u/∂y  =  -  ∂v/∂x,  Kirchhoff  en  sus  investigaciones  denominó  a  la variable u  potencial  electrostático. Encontró  una  generalización  de  la  solución  de  Helmholtz  para  la  ecuación de ondas, de la que una aplicación se denominó principio de Huygens de la acústica. Escribió Lecciones de física matemática (cuatro volúmenes, 1876-1894)

Whitworth

E<

l matemático inglés y sacerdote de la Iglesia de Inglaterra William Allen Whitworth como estudiante de pregrado,  se convirtió en el editor fundador en jefe del Messenger of Mathematics, y continuó como su editor hasta 1880. Publicó trabajos sobre la espiral logarítmica y las coordenadas trilineales, pero su publicación matemática más famosa es el libro Choice and Chance. : Tratado elemental sobre permutaciones, combinaciones y probabilidad (publicado por primera vez en 1867 y ampliado a varias ediciones posteriores). La primera edición del libro trataba el tema principalmente desde el punto de vista de los cálculos aritméticos, pero tenía un apéndice sobre álgebra y se basaba en conferencias que había dado en el Queen's College. Las ediciones posteriores agregaron material sobre combinatoria enumerativa (el número de formas de organizar elementos en grupos con varias restricciones), trastornos, probabilidad frecuentista, esperanza de vida,
Entre las otras contribuciones de este libro, Whitworth fue el primero en utilizar números de Bell ordenados para contar el número de ordenamientos débiles de un conjunto, en la edición de 1886. Estos números habían sido estudiados anteriormente por Arthur Cayley, pero para un problema diferente. Fue el primero en publicar el teorema de la balota de Bertrand, en 1878; el teorema lleva mal el nombre de Joseph Louis François Bertrand, quien redescubrió el mismo resultado en 1887. Es el inventor de la notación E [X] para el valor esperado de una variable aleatoria X, todavía en uso común, y acuñó el nombre " subfactorial "para el número de alteraciones de n elementos.
Otra de las contribuciones de Whitworth, en geometría, tiene que ver con formas equitativas, formas cuya área tiene el mismo valor numérico (con un conjunto diferente de unidades) que su perímetro. Como mostró Whitworth con D. Biddle en 1904, hay exactamente cinco triángulos iguales con lados enteros: los dos triángulos rectángulos con longitudes laterales (5,12,13) ​​y (6,8,10), y los tres triángulos con longitudes laterales (6,25,29), (7,15,20) y (9,10,17)

Murphy

El matemático británico Robert Murphy fue miembro de la universidad de Cambridge. Escribió Principios elementales de las teorías de electricidad, calor y acciones moleculares (1833), donde reunió algunos viejos resultados de los polinomios de Legendre y obtuvo algunos nuevos, presentándolos de forma sistemática, y demostró que cualquier función puede desarrollarse en términos de dichos polinomios aplicando la integración término a término y la propiedad de la ortogonalidad (teorema integral). Ordenó y amplió (1837) las ideas de Servois sobre la conservación de ciertas leyes formales en el cálculo diferencial con distintos símbolos operatorios.

Jung

Heinrich Wilhelm Ewald Jung fue un matemático alemán especializado en geometría y geometría algebraica. Estudió matemáticas, física y química en la Universidad de Marburg y la Universidad de Berlín.
Durante la República de Weimar , Jung fue miembro de la antirrepublicana Alldeutschen Verband y también de Der Stahlhelm . En la era nazi, Jung fue miembro de Nationalsozialistischen Volkswohlfahrt (NSV), Nationalsozialistischer Deutscher Dozentenbund (NSDDB) y Nationalsozialistischerhonore.

Jung desarrolló una teoría general de las funciones theta con su maestro Schottky. Su teoría aritmética de funciones algebraicas en dos variables es la principal fuente de su fama. También aplicó su teoría a superficies algebraicas y trabajó en transformaciones birracionales. La investigación original de Jung en esta teoría se reúne en su libro "Einführung in die algebraische Theorie der Funktionen von ... zwei Veränderlicher.