Matemalescopio

​¡ Qué poema el análisis del número áureo!.

Paul Valery

 Matemáticos que han nacido o fallecido el día 13 de Abril

Curiosidades del día

• Hoy es el centésimo cuarto día del año.
• 104 tiene 8 divisores cuya suma es 210
• 104 es un número abundante pues la suma de sus divisores positivos, excepto el mismo, es mayor que él.
• 104 es un número tau pues es divisible por la suma de sus dígitos.
• 104 es un número pernicioso pues su expresión binaria contiene un número primo de unos, 1101000.
• 104 es un número cortés pues puede expresarse como suma de naturales consecutivos  2 + ... + 14
• 104 es un número primitivo abundante pues es menor que la suma de sus divisores propios, ninguno de los cuales es abundante
• 104 y su siguiente 105 forman un par de  Ruth-Aaron pues la suma de sus distintos factores primos es la misma 15
• 104 es un número odioso pues su expresión en binario posee un número impar de dígitos
• La inversión de 104 es un número primo.
• 104 es suma de ocho pares consecutivos 104=6+8+10+12+14+16+18+20
• 104 es un número práctico pues todos los naturales menores que él pueden escribirse como suma de distintos divisores de 104

Tal día como hoy del año:

1625, la palabra "microscopio" fue acuñada como término sugerido en una carta escrita por Johannes Faber de Bamberg, Alemania, a Federigo Cesi, duque de Aquasparata y fundador de la Accademia dei Lincei (Academia del Lince) de Italia. Esta Academia, posiblemente la primera sociedad científica del mundo, tomó su nombre del animal por su visión excepcional.

1668, Lord Brouncker, presidente de la Royal Society, publica "el primer resultado matemático que se publicará en una revista matemática" en las transacciones filosóficas de la Royal Society. Su demostración del método de cuadratura de la hipérbola rectangular, y = x ^-1 amplió el trabajo de Wallis en Arithmetica infinitorium. 

1672, Después de presentar su artículo sobre la composición de la luz como una “mezcla heterogénea de rayos refrangibles diferentes” el 19 de febrero, surgieron varios críticos, sobre todo Robert Hooke. Newton respondió a las críticas con una carta a la Royal Society,

1759, Vuelve el cometa Halley, como predijo en 1682. El cometa alcanzó el perihelio por última vez el 9 de febrero de 1986, y volverá a alcanzarlo el 28 de julio de 2061

1791. Legendre es nombrado uno de los tres comisionados de la Academia Francesa para las operaciones astronómicas y triangulaciones necesarias para determinar el metro estándar. Los otros fueron Mechain y Cassini IV

Al- Karaji

Al-Karaji era ingeniero y matemático del más alto nivel. Aunque escribió apoyándose en el trabajo de matemáticos anteriores, es el primero que libera el álgebra de las operaciones geométricas, que eran fruto de la aritmética griega, para sustituirlas por el tipo de operaciones que constituyen la base del álgebra moderna.

  En sus trabajos sobre álgebra, dio las reglas de las operaciones aritméticas con polinomios. Se cree que es el primero que introdujo la teoría del cálculo algebraico. Al-Karaji investigó sobre los llamados coeficientes binomiales  y el triángulo de Pascal. También hizo uso el método de inducción para probar sus resultados.

Sus contribuciones al campo de las matemáticas y de la ingeniería todavía se reconocen hoy por sus trabajos sobre la tabla de coeficientes binomiales, su ley de la formación:

 la expansión 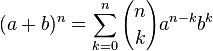para el número entero n.

Esto  hipótesis, históricamente, se le atribuye a Sir Isaac Newton. 

Frisi

El matemático  y astrónomo italiano Paolo Frisi  cursó sus estudios en monasterio barnabita de Milan  y posteriormente en el de Padua. A los veintiún años de edad, compuso un tratado sobre la figura de la Tierra, y la reputación que adquirió poco después llevó a que el rey de Sardinia le concediese el puesto de profesor de filosofía en la Universidad de Casale. Su amistad con Radicati, un hombre de ideas liberales, provocó que sus superiores clericales lo trasladasen a Novara, donde debió trabajar como predicador.

En 1753 fue elegido miembro de la Academia de Ciencias de París, y poco después comenzó a trabajar como profesor de filosofía en la Universidad Barnabita de San Alejandro en Milán. En esta época, un joven jesuita lo atacó cuando estaba realizando una disertación sobre la figura de la Tierra, lo que lo llevó a enemistarse con dicho grupo y a aliarse con sus enemigos, como Jean d'Alembert, Nicolas de Condorcet y otros enciclopedistas. En 1756 Leopoldo, Gran Duque de Toscana, le concedió el cargo de profesor de matemática en la Universidad de Pisa, donde permanecería durante ocho años

Su conocimiento sobre hidráulica causó que fuese consultado con frecuencia con respecto al manejo de los canales y otros cursos de agua en varias partes de Europa. Fue debido a sus conocimientos que pudieron introducirse en Italia los pararrayos para la protección de los edificios.

 El matemático americano, de origen polaco, Stanislaw Ulam ayudó a desarrollar la teoría que permitió la bomba de hidrógeno. Contribuyó también a estudios más pacíficos como la conjetura de Syracusa (conjetura de Ulam), la espiral de los números primos (espiral de Ulam), los números de la suerte.Estudiante precoz, comenzó a estudiar matemáticas por su cuenta a los 14 años. En 1933 se doctoró en el Instituto Politécnico de Lwów. En 1935, invitado por el matemático húngaro John von Neumann, pasó unos meses en el Instituto de Estudios Avanzados de Princeton; trabajó después en la Universidad de Harvard, primero como becario y después como profesor. Durante esta época, pasaba los veranos en Polonia. En el verano de 1939 salió de Polonia con su hermano Adam un mes antes del inicio de la Segunda Guerra Mundial; fueron los únicos miembros de su familia que se salvaron del Holocausto. De nuevo en los Estados Unidos, en 1940 ya era profesor asistente en la Universidad de Wisconsin, y en 1943 obtuvo la nacionalidad estadounidense. Ese mismo año, su amigo John von Neumann le invitó a participar en un proyecto de guerra secreto en Nuevo México. Ulam descubrió la importancia de ese proyecto cuando tomó prestado un libro sobre Nuevo México en la biblioteca de la universidad y descubrió en la tarjeta de préstamo los nombres de varios científicos que habían desaparecido recientemente del campus; decidió participar, y así se unió al Proyecto Manhattan, que estaba desarrollando la bomba atómica. En el Proyecto Manhattan propuso la utilización del método de Monte Carlo (un método estadístico basado en el uso de números aleatorios) para el cálculo de las complicadas integrales de la física nuclear, y resolvió el problema de cómo iniciar la fusión nuclear en la bomba de hidrógeno, bomba que diseñó y patentó junto con el físico húngaro Edward Teller. En palabras del físico alemán Hans Bethe, también participante en el proyecto, "Después de la construcción de la bomba H, los periodistas comenzaron a llamar a Teller el padre de la bomba H. Por el bien de la Historia, creo que es más preciso decir que Ulam es el padre, puesto que aportó la semilla, y Teller es la madre, puesto que se quedó con el hijo. En cuanto a mí, imagino que soy la comadrona." Después de la Segunda Guerra Mundial abandonó la matemática pura para dedicarse a un trabajo más especulativo, proponiendo problemas y realizando conjeturas, generalmente relacionados con la aplicación de las matemáticas a la física y a la biología. En 1947, Ulam concibió la propulsión nuclear pulsada para vehículos espaciales, el invento del que se sentía más orgulloso al final de su vida. También trabajó en muy diversos campos de la matemática pura, y fue uno de los primeros adeptos del uso de ordenadores para realizar simulaciones matemáticas. Entre sus contribuciones a la matemática pura está la enunciación del teorema de Borsuk-Ulam (demostrado por Karol Borsuk en 1933): Para toda función continua sobre la superficie de una esfera (en cualquier número de dimensiones), existen dos puntos antipodales (o sea, situado uno en las antípodas del otro) con el mismo valor de dicha función. Esto significa, por ejemplo, que en todo momento existen sobre la superficie de la Tierra dos puntos antipodales con la misma temperatura y la misma presión atmosférica. Durante una conferencia científica en 1963, Ulam realizó un curioso descubrimiento sobre los números primos. Aburrido, se puso a garabatear los números enteros en una espiral, comenzando por el 1 en el centro, y avanzando en sentido contrario al de las agujas del reloj. Al seleccionar los números primos, descubrió que éstos tienen tendencia a situarse en líneas diagonales. Es lo que se llama la espiral de Ulam.  

Emma Castelnuovo

La matemática italiana Emma Castelnuovo es hija de un gran geómetra italiano, Guido Castelnuovo. Obtuvo una plaza de profesora de secundaria en 1938, de la que fue desposeída unos días más tarde en aplicación de las leyes raciales de Mussolini. Durante la guerra y la ocupación nazi de Italia impartió clases clandestinas de matemáticas de casa en casa, para refugiados y perseguidos. En 1944, al finalizar la guerra, fue rehabilitada y comenzó a trabajar en el Instituto Tasso de Roma, en el que permaneció hasta su jubilación en 1979. Desde 1946 escribe numerosos artículos y libros sobre El Método Intuitivo para enseñar Geometría en el Primer Ciclo de Secundaria. Con los que sorprende por sus ideas y métodos novedosos en esta época: “…el curso de geometría intuitiva debe suscitar, a través de la observación de miles de hechos, el interés del alumno por las propiedades fundamentales de las figuras geométricas y el gusto por la investigación. Este gusto nace haciendo participar al alumno en el trabajo creativo.…” Es muy destacable que Emma Castelnuovo, por decisión propia, ha enseñado siempre en la Escuela Secundaria de primer ciclo, para alumnos entre 11 y 14 años. Y en la última reforma de la Secundaria Italiana, en 1979, Emma tiene una gran influencia. Esta reforma fue precedida de un movimiento de renovación en la educación matemática, promovido por diversas iniciativas personales y organismos oficiales. Un ejemplo de esta renovación es la colección de didáctica de las matemáticas dirigida por Emma Castelnuovo. Actualmente su influencia sigue vigente a través de muchos de sus discípulos que se ocupan de la formación metodológica y puesta al día de los profesores en el “Laboratorio Didáctico” del Instituto Matemático de Roma.

Severi

El matemático  italiano Francesco Severi,  nació  en  Arezzo.  Trabajó  en  geometría  algebraica, geometría birracional, teoría de superficies algebraicas y de las curvas trazadas sobre ellas, teoría de espacios modulares, teoría de funciones de varias variables complejas.Inicio la carrera de ingeniería en la Universidad de Turín . Sin embargo, debido principalmente a la influencia ejercida por la enseñanza de Corrado Segre , comprendió de inmediato que su verdadera inclinación era por las matemáticas , por lo que cambió la dirección de los estudios en este sentido y se graduó en matemáticas en 1900 , con una tesis sobre geometría enumerativa, tema que no abandonará en su carrera posterior. Fue asistente de Enrico D'Ovidio y, de 1902 a 1905, realizó el curso de geometría proyectiva y descriptiva como profesor libre. Más tarde se mudó a la Universidad de Bolonia como asistente de Federigo Enriques , luego a la Universidad de Pisa , como asistente de Eugenio Bertini . En 1904 , gracias a los importantes resultados obtenidos por él en geometría enumerativa y en geometría biracional de superficies algebraicas , obtuvo la cátedra de geometría descriptiva y proyectiva en la Universidad de Parma .En 1908, durante la ceremonia inaugural del IV Congreso Internacional de Matemáticos celebrado en Roma, recibió la Medalla Guccia. en 1931 prestó juramento de fidelidad al fascismo . En su autobiografía From Science to Faith (1959), reconoció, mirando retrospectivamente en su pasado político los veinte años fascistas, que "las matemáticas son el arte de dar el mismo nombre a diferentes cosas: por lo tanto, los matemáticos a menudo cometen errores al tratar con  la política, ya que la política es, en cambio, el arte de dar diferentes nombres a las mismas cosas ». En 1938 , fue uno de los fundadores del Instituto Nacional de Alta Matemática en Roma, una institución de gran prestigio internacional e importancia para las matemáticas italianas, que más tarde recibió su nombre. Sus resultados en matemáticas son numerosos y casi todos de alto calibre. Deja contribuciones significativas en la geometría enumerativa y proyectiva , en la teoría de las funciones analíticas de varias variables complejas, en la de las variedades abelianas y cuasiabelianas , y, sobre todo, en diversos sectores de la geometría algebraica , en particular en relación con las propiedades de las superficies y de las variedades algebraicas invariantes para las transformaciones biracionales , un tema que ya ha sido abordado por Guido Castelnuovo y Federigo Enriques con quienes establecerá, junto con otros matemáticos italianos, la escuela italiana de geometría algebraica , de renombre internacional, que atrajo a matemáticos que se hicieron famosos en el extranjero, incluyendo Oscar Zariski y André Weil 

Fowler

El matemático, inglés,  e historiador de la matemática griega David Herbert Fowler  trabajó sobre la teoría de la razón pre-eudoxiana, –el filósofo griego Eudoxo de Cnido enunció los conceptos de razón y proporcionalidad para determinar la medida de magnitudes arbitrarias– usando el proceso de antifairesis.

Fowler cuestionó la historia estándar del descubrimiento matemático griego, en el que se argumenta que el hallazgo del fenómeno de la inconmensurabilidad supuso una conmoción. Fowler opinaba que, al no disponer de los conceptos de número real o de división, los griegos tuvieron dificultades para definir con rigor la noción de razón, que ellos llamaban logos. El Libro V de Euclides es una exposición de la teoría de la proporción de Eudoxo, que conseguía decidir cuando dos razones eran iguales, sin tener que definirlas. Su teoría tuvo tanto éxito que acabó con las teorías anteriores: el objetivo de Fowler fue el de encontrar pruebas del redescubrimiento de estas teorías previas.

En particular Teeteto introdujo una definición de ratio llamada antifairesis, basada en el algoritmo de Euclides.

Fowler desarrolló sus ideas en una serie de artículos que le llevaron a la publicación de The Mathematics of Plato’s Academy: A New Reconstruction en 1987.

Cannon

La Astrónoma sorda estadounidense Annie Jump Cannon estaba especializada en la clasificación de espectros estelares. En 1896 fue contratada en el Observatorio de la Universidad de Harvard, permaneciendo allí durante toda su carrera. El sistema de clasificación espectral de Harvard fue desarrollado por primera vez por Edward C. Pickering, Director del Observatorio, alrededor del cambio de siglo utilizando espectros de prismas objetivos tomados en placas fotográficas mejoradas. En conjunto con Pickering Cannon, se desarrolló, perfeccionó e implementó aún más el sistema de Harvard. Reorganizó la clasificación de las estrellas en términos de temperatura superficial en las clases espectrales O, B, A, F, G, K, M y catalogó más de 225.000 estrellas para el monumental Catálogo de espectros estelares de Henry Draper

Gregory

 El matemático escocés Duncan Farquharson Gregory fue uno de los primeros en investigar las ideas modernas del álgebra abstracta. En este trabajo, Gregory construyó sobre los cimientos de Peacock pero fue muy lejos más hacia el álgebra moderna. Gregory, a su vez, tuvo una gran influencia en Boole y fue a través de su influencia que Boole inició su investigación innovadora

Fue profesor en el Trinity College de Cambridge. Fue el primero en dar   las   leyes   correspondientes   a   los   conceptos   conmutativo,   distributivo   y   asociativo   (1838).   Perteneció al grupo de los britanes que se esforzaban en crear un álgebra simbólica. En su obra Sobre la verdadera naturaleza del álgebra simbólica (1840), escribió: “La luz a la que consideraré el álgebra simbólica  es  como  la  ciencia  que  trata  la  combinación  de  las  operaciones  definidas,  no  por  su  naturaleza,  esto  es,  por  lo  que  son  o  lo  que  hacen,  sino  por  las  leyes  de  las  combinaciones  a  las  que  están  sujetas...  Es  cierto  que  estas  leyes  han  sido  en  muchos  casos  sugeridas  (como  Mr.  Peacock  ha  dicho convenientemente) por las leyes conocidas de las operaciones de los números, pero el paso dado del álgebra aritmética a la simbólica es que, dejando de lado la naturaleza de las operaciones que los símbolos  que  usamos  representan,  suponemos  la  existencia  de  clases  de  operaciones  desconocidas  sujetas a esas mismas leyes. Así somos capaces de probar ciertas relaciones entre las diferentes clases de operaciones, que, cuando son expresadas entre los símbolos, se llaman teoremas algebraicos”. Otras obras suyas: Ensayo de fundamentos del álgebra (1838), Colección de ejemplos de los procedimientos del  cálculo  diferencial  e  integral  (1841).  Fundó  el  Cambridge  Mathematical  Journal  (1839-1843)

Maddison

Isabel Maddison fue una matemática inglesa más conocida por su trabajo sobre ecuaciones diferenciales.

Fue amiga y compañera de Grace Chisholm (después sería Grace Chisholm Young) en el Girton College: ambas recibieron clases de Arthur Cayley, Alfred North Whitehead y William Young.

Defendió su tesis doctoral en el Bryn Mawr College en 1896: Singular solutions of differential equations of the first order in two variables and the geometric properties of certain invariants and covariants of their complete primitives, bajo la dirección de Charlotte Scott.

Es sobre todo conocida por su trabajo en ecuaciones diferenciales. Su artículo On certain factors of c- and p- discriminants and their relations to fixed points in the family of curves publicado en el  Journal of Pure and Applied Mathematics –basado en su tesis– recibió el Premio Gambel

Schlömilch

El matemático alemán Oskar Schlömilch estudió matemáticas y filosofía en Jena, Berlín y Viena. Enseñó en Jena, y fue catedrático de matemáticas superiores y mecánica analítica en el Instituto Técnico de Dresde (1849). Fue director general de la enseñanza profesional en Sajonia, hasta 1885. Llevó a cabo un estudio riguroso de las funciones elementales. Publicó Características de la representación científica de la geometría , Manual de cálculo diferencial e integral (1847), Cálculo de diferencias finitas (1848). Manual de análisis algebraico (1851), Geometría analítica (1855), Manual de mecánica analítica , Aforismos filosóficos de un matemático (1877), Manual de matemáticas (1879-1881), Compendio de análisis superior (1881), Geometría analítica del espacio (1888).

Weldon

Walter Frank Raphael Weldon, generalmente llamado Raphael Weldon, fue un biólogo evolutivo inglés y uno de los fundadores de la biometría. Fue el editor fundador conjunto de Biometrika, con Francis Galton y Karl Pearson.  Pearson dijo de él: "Era un poeta por naturaleza, y estos dan lo mejor a la ciencia, porque dan ideas

Su enseñanza fue descrita en estos términos brillantes:
Rara vez se le da a un hombre enseñar como enseñó Weldon. Daba conferencias casi como alguien inspirado. Su extrema seriedad sólo fue igualada por su lucidez. Despertaba entusiasmo hasta en los más aburridos, y poseía el don divino del interés apremiante.

 Su trabajo pronto comenzó a involucrar el análisis estadístico. Fue conducido en esta dirección por el trabajo de Galton sobre la herencia natural. Extendió el análisis estadístico que Galton y Quetelet habían aplicado a los humanos a otras especies zoológicas. Al darse cuenta de que sus habilidades matemáticas eran algo menores de lo que deseaba, Weldon leyó mucho y estudió, en particular, las principales obras de los matemáticos franceses sobre el cálculo de probabilidades .. Su trabajo involucró el estudio de coeficientes de correlación para la relación entre medidas de órganos en animales y es importante para los inicios de la biometría.

Molyneux

Samuel Molyneux fue un astrónomo británico (Observatorio Real de Kew) y político. Con su asistente James Bradley, realizó mediciones de la difracción, la curvatura de la luz de las estrellas. Observaron la estrella Draconis con un telescopio vertical. Ya en 1725, tenían evidencia del movimiento de la Tierra que respalda el modelo copernicano de la Tierra girando alrededor del sol. La estrella oscila con un período de 39 segundos de arco entre su punto de oscilación más bajo en mayo y su punto de oscilación más alto en septiembre. . En 1728, sufrió un ataque mientras estaba en la Cámara de los Comunes. Fue tratado por el anatomista de la corte Nathaniel St André , pero el tratamiento no tuvo éxito y Molyneux murió en Kew en abril. En la noche de la muerte, St André se fugó con la esposa de Molyneux, Elizabeth, y los dos se casaron en 1730. Samuel Madden , un pariente de Molyneux, afirmó que St André había envenenado al diputado. Aunque St André ganó una acción por difamación , se encontró incapaz de conseguir un trabajo regular.

Hart

Sir Andrew Searle Hart fue un matemático angloirlandés, vicecanciller del Trinity College de Dublín y autor de tesis sobre hidrostática y mecánica, así como de artículos sobre geodesia

Asistió al Trinity College de Dublín en 1828 y se convirtió en compañero de clase y amigo íntimo de Isaac Butt, con quien siempre mantuvo una buena amistad, a pesar de sus diferencias políticas. Hart se graduó en 1833 y recibió su maestría en 1839; Completó su licenciatura y doctorado en 1840. Fue elegido miembro del Trinity College de Dublín en 1835, miembro en 1858 y vicerrector en 1876.

Tiene un interés activo en los asuntos de la Iglesia de Irlanda y durante muchos años fue miembro de la Asamblea General de la Iglesia y del órgano representativo de la Iglesia. Alcanzó gran fama como matemático y publicó tratados útiles sobre hidrostática y mecánica. Entre 1849 y 1861 escribió interesantes artículos en Cambridge y Dublin Mathematical Journals, Proceedings of the Irish Academy y Mathematical Quarterly Journal, principalmente sobre el tema de la geodesia y las curvas. En 1886 fue nombrado caballero por el teniente Lord Carnarvon en el castillo de Dublín, "en reconocimiento a su rango y expediente académico". 

Boncompagni

El matemático italiano Baldassarre Boncompagni  fue un destacado historiador de las matemáticas. Creó su propia editorial y publicó su propia revista sobre la historia de las matemáticas desde 1868 hasta 1887. Fue el encargado de dar a conocer la importancia de Leonardo Fibonacci para la historia de las matemáticas. Boncompagni editó Bullettino di bibliografia e di storia delle scienze matematiche e fisiche ("El boletín de bibliografía e historia de las ciencias físicas y matemáticas") (1868-1887), la primera publicación periódica italiana enteramente dedicada a la historia de las matemáticas. Editó todos los artículos que aparecían en la revista. También preparó y publicó la primera edición moderna del Liber Abaci de Fibonacci

​Sadosky

​El matemático y físico argentino Manuel Sadosky estudió en el Instituto Henri Poincaré de París y en el Instituto del Cálculo de Roma gracias a una beca. Allí se especializó en matemática aplicada. De regreso a Buenos Aires, dio clases en el Instituto Radiotécnico hasta 1953. Fue Docente en la UBA, en la Facultad de Ingeniería y en la de Ciencias Exactas, donde ocupó el puesto de Vicedecano y en la UNLP. Hacia fines de la década del ‘50, comenzó a interesarse y a estudiar computación.

En 1960, creó el Instituto de Cálculo, donde instaló la primera computadora que tuvo el país, Clementina. Como consecuencia, una gran cantidad de profesionales pudieron formarse en la especialidad de computador científico, carrera pensada y creada por él. Fue pionero de la docencia en computación tanto en Argentina, como en Uruguay y Paraguay. Propulsó la creación de la Escuela Superior Latinoamericana de Informática (ESLAI). En 1967 creó en Uruguay el Instituto de Cálculo de Montevideo en la Universidad de la República, donde fue declarado Doctor Honoris Causa. Desde 1974 hasta 1979 trabajó en el Instituto Cendes de la Universidad Central de Venezuela y luego en el Museo de Ciencias de Barcelona. Impulsó la Fundación Alberto Einstein para becar a estudiantes físico-matemáticos. De ésa época son sus dos libros: Cálculo numérico y gráfico y Cálculo diferencial e integral (junto a Rebeca Guber).

Durante su exilio, debido a la dictadura militar, brindó sus servicios a los países que lo recibieron: Uruguay, Colombia, Venezuela y España. Con el retorno de la democracia fue Secretario de Ciencia y Técnica durante el Gobierno de Raúl Alfonsín. Siempre continuó vinculado a la Universidad de Buenos Aires, donde fue declarado Profesor Emérito (1985).

Fue Premio Konex de Honor 2006

​